Complexity Analysis (2) - Asymptotic Analysis (점근적 분석)

서문 (Preface)

지난 포스팅에서는 알고리즘의 정의와, 효율성을 분석하는 방법, 그리고 알고리즘의 복잡도를 시간과 공간적인 측면에서 수학적으로 기술할 수 있다는 것에 대해 알아봤습니다. 그리고 이번 포스팅에서의 주제는 이걸 확장시켜서 구체적으로 어떤 방법을 통해 복잡도를 기술할 수 있는지를 다루도록 하겠습니다.

 

복잡도의 점근적 분석 (Asymptotic Analysis)

점근적 분석이란, 자료의 갯수 $n$ 값이 커질수록 이에 따라 $n$ 에 관한 어떤 알고리즘의 복잡도가 어떤식으로 변화해 나가는지를 의미합니다. 이 때, 충분히 큰 $n$ 에 대하여 주어진 $n$ 에 관한 함수 $f(n)$ 을 또 다른 함수 $g(n)$ 을 통하여 나타낼 수 있는데, ($g(n)$ 을 $f(n)$ 과 충분히 비슷한 함수라고 가정합시다) 구체적으로는:

$$f(n)\sim g(n)(n\ge n_0,n\to \mathrm{\infty })$$

 

해석을 하자면, $n_0$ 이상인 모든 $n$ 에 대하여 (충분히 큰 $n$), $n$ 이 증가함에 따라 $f(n)$ 값이 $g(n)$ 에 근접해간다는 뜻입니다. 이때 $\sim$ 를 좀더 정확하게 기술하면:

$${\displaystyle \underset{n\to \mathrm{\infty }}{lim}\frac{f(n)}{g(n)}=1(\mathrm{\forall }n⩾n_0)}$$

 

즉, 충분히 큰 $n$ 이 무한히 증가함에 따라 두 함수의 함숫값의 격차가 1에 수렴한다는 뜻이죠. (같아진다는 말입니다)

 

예를들어 보자면, 충분히 큰 $ n $ 값에 대해, $n$ 이 증가함에 따라  $f(n)=10n^3-100n$ 과 $g(n)=n^3$ 의 격차가 점점 줄어들어 1에 가까워지는 것을 것을 알 수 있습니다.

 

Big-O Notation (Big-O 표기법)

위에 서술한 내용을 좀 더 간단히 표현하기 위해 수학자들은 몇가지의 표기법을 도입했는데요, 그 중 제일 대표적인 것이 바로 Big-O 표기법입니다. 이번 주제는 직관적인 설명을 위해 좀 더 예시를 통해 설명을 하겠습니다.$n$ 에 관한 두 함수 $f(n)=5n^3-20n^2-10n+5$ 와 $g(n)=n^3$ 이 있을 때, 이 두 함수의 그래프는 아래와 같이 그려집니다 (파란색이 $f$, 빨간색이 $g$ 입니다):

figure 1. 두 함수 f, g 의 그래프

 

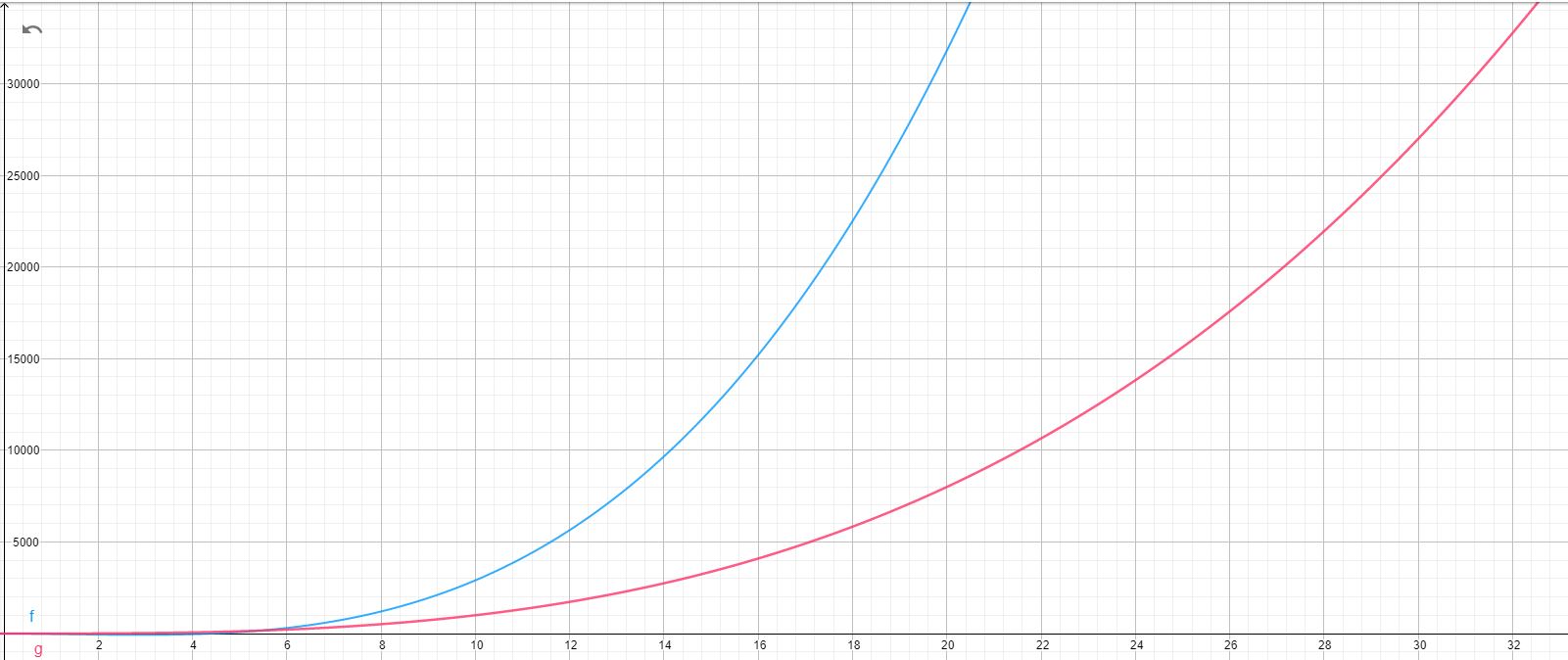
이 때, 두 함수는 결국 비슷한 증가 양상 (Trend) 을 보이므로 (다항함수이기 때문에 최고차항이 결국 전체 결과값을 지배하게 됩니다) 함수 $g$ 에 어떤 상수 $c$ 를 곱하게 되면 충분히 큰 $n$ 값에 대하여, $g(n)$ 값을 $f(n)$ 이상으로 만들 수 있습니다. 위 두 함수의 경우에는 이때 이 $c$ 값을 5로 두면, $n$ 이 대략적으로 2 이상일 때 (이 때의 $n$ 값을 $n_0$ 라고 표현합니다), $g(n)$ 은 아래와 같이 $f(n)$ 보다 커지게 됩니다:

figure 2. 함수 f 보다 커지는 g

 

다시 말해, 어떤 함수 $f(n)$ 이 주어져 있을 때, 비슷한 증가 양상을 보이는 함수 $g(n)$ 를 정의 내릴 수 있고, 이 때 어떤 상수 $c$ 가 정의되면, 충분히 큰 $n$ 값에 대하여 $c\cdot g(n)$ 이 $f(n)$ 보다 크거나 같을 때, $f(n)=O(g(n))$ 이라고 표기합니다.

 $$f(n)=O(g(n))\iff \mathrm{\exists }c:f(n)⩽c\cdot g(n)(\mathrm{\forall }n⩾n_0)$$

 

그래서 무슨 뜻인데?

자 수학 기호가 많이 등장을 해서 순간 당황하셨을 거라 생각합니다. 그렇지만 위의 식을 하나하나 뜯어보면 이해하는게 크게 어렵지 않다는걸 알 수 있습니다. 다시 말해:

$n$ 에 관한 두 함수 $f$ 와 $g$ 가 정의될 때, 충분히 큰 모든 $n$ 에 대하여  ($n⩾n_0$)
$cg(n)$ 을 항상 $f(n)$ 보다 크거나 같게 만드는 어떤 상수 $c$ 가 존재하면,
이 때 $f(n)$ 을 $O(g(n))$ 이라 표기한다.

 

자 그러면 위의 예시로 돌아가서 대입을 해봅시다. $f(n)$ 을 $f(n)=5n^3-20n^2-10n+5$  로, $g(n)$ 을 $g(n)=n^3$ 로 정의 했었고, 위의 조건을 만족하는 $c$ 값 이 존재하므로, 각각 대입하면: $5n^3-20n^2-10n+5=O(n^3)$ 이 나오게 됩니다.

이 때, $f(n)$ 을 어떤 알고리즘 A 의 시간 복잡도라고 생각하면, 이 알고리즘의 시간 복잡도는 $O(n^3)$ 이라고 기술할 수 있게 되는거죠.

결국 위 과정을 통해 저희가 얻어낸 것은 복잡한 함수로 정의되는 알고리즘의 복잡도를 중요하지 않은 부분을 생략해서 단순화 시켜 나타낼 수 있다는 말인 것이죠. 이를 통해 서로 다른 알고리즘들의 복잡도가 Big-O 를 이용해 같은 함수로 표현될 수 있다면, 이 둘의 "복잡도가 같다, 즉 효율성이 같다" (혹은 비슷하다) 라고 정의를 내릴 수가 있게됩니다.

 

다항함수 (Polynomial Functions) 의 복잡도의 Big-O 표현

앞으로의 편의를 위해 좀 더 일반화를 해봅시다. 단순히 위에서 본 $n^3$ 뿐만 아니라 위 방식을 최고차항을 어떤 실수 $k$ 로 갖는 모든 다항함수에 적용시킬 수 있지 않을까요?

 

아래와 같이 일반화된 형태의 최고차항이 $k$ 인 다항함수 $T(n)$ 이 주어질 때:$$T(n)=a_k{n}^k+a_{k-1}{n}^{k-1}+\cdots +a_{1}n+a_0=\sum _{i=0}^k{a}_i{n}^i$$

 

이 충분히 큰 $n⩾n_0$ 에 대하여 $T(n)⩽c{n}^k$ 를 성립시키는 상수 $c$ 값을 찾을 수 있으므로, (엄밀한 증명을 원한다면 proof by contradiction 을 이용해봅시다. 즉, c 값이 존재하지 않는다고 가정하면 단순하게는 어떤 $n$ 과 $c$ 를 찾아서 이 역이 성립하지 않음을 증명할 수 있겠죠) $T(n)=O(n^k)$ 가 성립하죠. 따라서, 이 $T(n)$ 형태의 시간 복잡도를 갖는 어떤 알고리즘이든 전부 $O(n^k)$ 의 시간 복잡도를 갖는다고 표현할 수 있다는 뜻입니다.

(즉, 앞으로 나오는 알고리즘들에서 다항함수 형태의 복잡도를 가질 때, 저희는 Big-O 를 이용해 단순화된 표기를 할 수 있다는 말이죠)

위의 일반화와 비슷한 방식을 다른 형태의 함수 (지수, 로그 등) 에도 적용시킬 수 있습니다. 해당 케이스들은 다음에 다루도록 하겠으나 궁금하다면 직접 찾아보거나 증명을 해보는 것도 좋은 방법입니다.

 

기타 Big-O 의 성질

$n$ 에 대한 함수 $f_1,f_2,g_1,g_2$ 에 대하여 $f_1(n)=O(g_1(n))$ 이고, $f_2(n)=O(g_2(n))$ 일때, 다음이 성립합니다:

$$f_1(n)\cdot f_2(n)=O(g_1(n)\cdot g_2(n))$$

(즉, 두 함수의 곱에 Big-O 를 씌우면 각각의 Big-O 로 bounded 되는 함수들의 곱에 Big-O 를 씌운 것과 같습니다.)

$$f_1(n)+f_2(n)=O(max(g_1(n),g_2(n)))$$

(두 함수를 합한 것의 Big-O 표현은 두 함수의 Big-O bounding 함수 중 큰 것에 Big-O 표현과 같습니다)

 

또, $n$ 에 대한 함수 $f$ 에 대하여 이 함수의 상수곱은 이 함수의 Big-O 표현에 영향을 주지 않습니다:

$$f(n)=O(g(n))\Rightarrow k\cdot f(n)=O(k\cdot g(n))=O(g(n))$$

 

이외의 Approximation (근사) 표현

Big-O 표현은 어떤 함수의 upper bound (즉, $f$ 가 $g$ 의 상수곱보다 항상 작거나 같아야 한다는 것을 명시함으로써, $f$ 의 증가 양상이 항상 $g$ 와 동일해야 한다는 것을 명시) 를 기술한다면, Big-O 외에도 아래와 같은 다양한 근사치를 나타내기 위한 표현들이 존재합니다:

 

Big-Omega Notation (Big-Omega 표기법)

오메가의 경우에는 Big-O 와 반대로 어떤 함수의 lower bound 를 알려주는 표현입니다. 즉, 두 함수 $f$ 와 $g$ 가 주어질 때, 충분히 큰 모든 $n$ 값에 대하여 항상 $f(n)⩾c\cdot g(n)$ 이 성립된다면 ($f$ 가 항상 $g$ 의 증가 양상 이상이라면) $f(n)=\mathrm{\Omega }(g(n))$ 이라 표기할 수 있습니다.

 $$f(n)=\mathrm{\Omega }(g(n))\iff \mathrm{\exists }c:f(n)⩾cg(n)(\mathrm{\forall }n⩾n_0)$$

 

Theta Notation (Theta 표기법)

마지막으로, theta 의 경우에는 어떤 함수의 증가 양상이 충분히 큰 모든 $n$ 값에 대하여 항상 다른 어떤 함수와 같아야 한다는 걸 표시합니다. 즉, 두 $n$ 에 관한 함수 $f$ 와 $g$ 가 있을 때, 충분히 큰 $n$ 값에 대해 $f(n)=O(g(n))$ 이고 동시에 $f(n)=\mathrm{\Omega }(g(n))$ 을 만족한다면, 이 $f$ 의 증가 양상을 theta 를 통해 $f(n)=\theta (g(n))$ 이라고 표현할 수 있습니다.

 $$f(n)=\theta (g(n))\iff \mathrm{\exists }{c}_1,c_2:f(n)⩾c_1\cdot g(n)\wedge f(n)⩽c_2\cdot g(n)(\mathrm{\forall }n⩾n_0)$$

 

요약 (Summary)

이번 포스팅에서는 새로운 수학적 표현들이 많이 등장해 살짝 당황스러우셨을수도 있을 것 같습니다. 그렇지만 지난번에도 언급했듯 수식은 결국 위의 정의한 내용들과 같은 말을 하는 것 뿐이니 앞으로 알고리즘을 분석하는데에 있어 Big-O, Big-Omega, 그리고 Theta 표기법이 어떤 뜻인지, 대략적으로만 이해하셔도 충분합니다. 그럼 다음 시간에는 좀 더 다양한 함수들로 표현되는 알고리즘의 복잡도와 예제들을 중점적으로 알아보도록 하겠습니다.